My Struggle With Velocity and Mom

Today is the birthday of Pafnuty Chebyshev born 1821 in Okatovo, Kaluga Region, Russia. Chebyshev investigated number theory, mechanics, and invented orthogonal polynomials.

Today's mathematician's quote is from G. Simmons who said "To isolate mathematics from the practical demands of the sciences is to invite the sterility of a cow shut away from the bulls."

The lives of my younger brother's are a study of contrast.  My younger brothers are identical twins. Their births were two minutes apart.  The oldest of the pair just recently became a grandfather while my "youngest" brother is teaching his 15 year old daughter how to drive. I was fortunate to have the majority of the driver's education instruction fall on the slender but resilient shoulders of my wife.

My real behind-the-wheel experience of learning how to drive fell on my mother. I have a number of experiences that I can recall during that time, many of them are not pleasant.  During the 1970's seat belts were in cars but were not used by anyone in my family except for the time I slammed on the brakes in the middle of a busy intersection catapulting my mother's head to the windshield of our banana colored 1972 Ford LTD.

This is the car that my brothers and I referred to as the "banana boat".

I am sixteen and have hair.

A constant discussion between my mother and myself was my obsession with speed and lack of the proper use of the "gas pedal".  The following sketch represents my mother's lament about the use of the accelerator.  She would often describe me as a "heavy foot" driver.

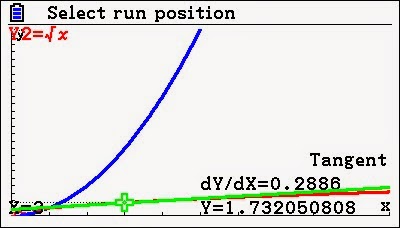
The graph that is labeled "Chuck" illustrates a quick gain of distance in a short period of time while the other graph labeled "Chuck's mom" indicates a gradual gain of distance in a greater time span.  Both of these graphs are defined as position functions.  They depict the distance traveled over an interval of time.  The graphs are both increasing; one quickly, the other gradually both they differ in terms of mathematicians call concavity. The "Chuck" graph is concave up and my velocity is increasing.  In calculus, velocity can be viewed as the slope of a line tangent to a position curve. I have examples below.

Notice for the same time value, x = 3, the slope of the green line on the upper graph is 0.2886 and the lower graph it is 6. When time increases as in the next two graphs, the slope decreases to 0.25 in the upper graph but increases to 16 in the lower graph.

In the upper graph, my velocity has decreased for another unit of time.  I have negative acceleration. My mother is relaxed, viewing the dafodils blooming in the neighbor's garden, and sets aside the belt buckle she had placed in her lap.  I turn down the volume on the radio as Perry Como  sings "Mama Loves Mambo".

In the lower graph, my velocity has increased for another unit of time.  I have positive acceleration. My mother has been forced further back into her seat, her eyes are closed, her teeth are clenched, and she is gripping tightly to the door handle.  I, on the other hand, have the window open, and am looking for tanned coeds that are enthralled by the power in front of me.

When velocity and acceleration have the same signs (they are both positive or both negative), speed is increasing.  When velocity and acceleration have opposite signs, speed is decreasing.  Here is another example.

This is a graph of two velocity functions.  Each graph is moving towards the x-axis.  On the x-axis, each will have a value of zero so each velocity function is decreasing.

The slopes of the lines tangent to each of these graphs represents the acceleration of an object at a particular time, x.

These diagrams indicated that the acceleration is decreasing (-2 to -3),velocity is positive, and speed is decreasing.

The above diagrams show that acceleration is increasing, velocity is negative, and again speed is decreasing.

I have mellowed out in my quest for speed. I have become accustomed to letting the other drivers pass me by while I reflect on the mathematics I see around me.  :-)

Tractor, Slide Rule, Calculator, and The Digital World

Today is the birthday of Heinrich Jung born 1876 in Essen, Germany.  Jung made contributions in the field of algebraic functions.

Today's quote is from Herbert Turnbull.  He quipped, "The usefulness of mathematics in furthering the sciences is commonly acknowledged: but outside the ranks of the experts there is little enquiry into its nature and purpose as a deliberate human activity."

My dad and I were having a discussion about innovation.  He grew up in South Dakota in the 1920's and 30's during the Dust Bowl.  He remarked to me that he remembered the turmoil that a purchase of a tractor caused among neighboring farmers.  I found an article that supported his perspective of that time. There are very few farmers that would subsist without the tractor.

When I was in high school our choice of a calculating device was the slide rule.  I still have my slide rule but am no longer proficient in using it.  The logarithmic concepts on which it is based have stayed with me.  The terms, mantissa and characteristic, have remained a common part of my vocabulary. :-)  I did not use a calculator my high school mathematics classes even though the scientific calculator existed.  I have colleagues that are approximately my age and they did use calculators in their high school math classes. I attributed my lack of technology to my mathematics teacher.  He was an excellent teacher and was a strong influence in my career path, I don't believe he was of the nature to jump to the latest "trend" in teaching.  He explained to me that he was confident that I would do well in college mathematics because the curriculum and instruction I received my K-12 experience built a solid foundation.

My parents purchased my first digital calculator as my high school graduation gift.  The cost was $150 and it was a Hewlett Packard 35s.   This calculator was in lieu of the traditional gift of suitcases.

I started collecting mechanic calculators a few years ago.  The image below is a particular model I purchased at a flea market.  A hardware/lumber yard store in my community has the same model on display.  Their calculator was the original adding machine used when the company was first established.

My current calculator of choice is the Casio Prizm FX-CG10.  This calculator has everything I want in a calculator.  The graphics are in color and has a minimal number of keystrokes needed to accomplish specific tasks.

Our school to transitioning to 1 to 1.  In mathematics, functions that are defined as 1 to 1 are those whose inverses are also functions.  In the classroom, 1 to 1 means that each student is equipped with a digital device.  As with any innovation, whether it is a tractor or a calculator there is a period of struggle to find its proper place.  As with tractors, there were losses and gains as the calculator entered the mathematics classroom.  Some mathematics concepts have fallen to the side while others have been advanced.  I used to teach linear interpolation as a method to approximate nonlinear results.  That topic is no longer applicable.  I am able to give more meaning to the richness of functions in graphic and tabular ways.  There are appropriate times to use the calculator in class but the use of the calculator exists and cannot be denied.  I believe the same will be true in 1 to 1 classrooms.  As educators, we will have our period of struggle, we will find appropriate times to use the devices in our classrooms but there is no denying that we are in a digital world and we must use all means available to us to engage our students.

When I Grow Up I Want To Be A . . . LOBSTER FISHERMAN

Today is the birthday of Vito Voterra born 1860 in Ancona, Italy.  Vito's work focused on partial differential equations with respect to the equation of cylindrical waves.  His major work was on integral equations.  

When I was in senior in high school I was still unsure what I wanted to be when I "grew up".  My mother wanted me to be a pastor and I was considering a career as a member of the Coast Guard or a mathematics teacher.  During my senior, we spent our Christmas visiting my sister in San Francisco. As we walked along the wharf, I had a moment of clarity.  I proudly remarked,"I want to be a LOBSTER FISHERMAN".  My mother erupted.  She explained to me in no uncertain terms, my destiny.  Her 60 inch frame grew as she became more agitated.  I was subdued and have never spoke to her again about lobster fishing.  I have visited the east coast many times and have watched the lobster boats come in to shore.  The life is tough and precarious.

Every year I assign a final project to my calculus students.  Their assignment is find the mathematics in what they love to do.  I have had projects on music, tennis, dance, skating, Rubik's Cube, whiffle ball, Escher, and bowhunting carp to name a few.  I, in turn, was wondering what mathematics existed in lobster fishing.  I found a mathematics game called "Lobster Pots", a mathematical article examining the exploitation of the lobster fisheries, a website sponsored by Gulf of Maine Research Institute that details all aspects of lobsters which contains mathematical activities pertaining to the career of a lobster fisherman, and the use of mathematical modeling in the optimization of productivity of the fishing industry.

I often tell the story of my lobster fishing yearning to my students.  A few years ago, Tyler, a student of mine, created this picture of me.  In addition to my math class, he was taking a digital photography class.  I am sure he was looking for lobsters but was resigned to use crabs from the show, "The Deadliest Catch".  The students still enjoy this picture and it finds its way on social media occasionally.  I particularly like the tattoos.

Happy Belated Birthday Rosie!

Today is the birthday of John Wilton born 1884 Belfast, Victoria, Australia.  Wilton's work focused on Analysis and Number Theory.

Today's quote is by mathematician Salomon Bochner.  He said, "The word 'mathematics' is a Greek word and, by origin, it means 'something that has been learned or understood,' or perhaps 'acquired knowledge,' or perhaps even, somewhat against grammar, 'acquirable knowledge,' that is, 'learnable knowledge,' that is, 'knowledge acquirable by learning."

Rosie is my dog.  She is a 55 pound labrador and poodle cross often referred to as a "labradoodle". On March 8th she completed her eighth year.  Her birthday celebration was brief.  The weather outside was not conducive to a long walk nor did the squirrels who were invited to the backyard attend her birthday party due to the nastiness of this year's winter.  According to the chart below, her age in "human years" is about 55 years.

Based on Rosie's age and weight, I used the orange graph and created the data plot below.

I used a graphing calculator's diagnostic capabilities to formulate an equation could be used to determine an human equivalent based on her age and weight.

The resulting formula is call a quartic function.    This particular function is f(x) = -0.001258x^4 + 0.05795529x^3 - 0.9158657x^2 + 11.0734406x + 1.17984189.  This function is just an estimate that is most accurate within the scatterplot.  The further the age moves beyond 20 actual years, the more inaccurate the function becomes.

I chose this particular model based on the Mean Squared error (MSe) of the regression.  This is a better indicator of fit that r^2 which is an analysis based on linear models.

Rosie is an awesome companion.  She is always excited to see me.  She is a great listener and has been a source of inspiration in developing scenarios of applied mathematics.  This school year has been the year of Rosie.  She has become somewhat of a cult hero.  I hope her health stays well and she continues to inspire students in my classroom.